Mathematicians have discovered that there exists an infinite number of potential shapes for black holes.
While a black hole’s surface is constrained to a sphere in three-dimensional space, in higher dimensions, there is an endless variety of arrangements that could exist.
In the observable universe, planets, stars, and black holes all tend to be spherical due to the gravitational attraction of gas and dust clouds towards the center of mass. In a universe with three dimensions of space and one of time, the event horizons of black holes are also theorized to be spherical. However, if there are higher dimensions that we cannot directly observe, could black holes take on different shapes?

Recent mathematical research suggests that in dimensions five and above, there could be an infinite number of configurations possible for black holes.
This theoretical work expands on earlier findings that indicated some exceptions to the spherical black hole rule. While it is uncertain whether these uniquely shaped black holes exist in nature, their detection could provide evidence of the universe’s higher dimensions. Future experiments, such as collisions at particle colliders, may reveal such discoveries.
Black Hole Doughnut
The tale of the possible shapes of black holes can be traced back to Stephen Hawking, who demonstrated in 1972 that the surface of a black hole, at a particular moment, must be a two-dimensional sphere, despite being a three-dimensional object. However, it wasn’t until the 1980s and ’90s, when string theory, which postulates the existence of up to 11 dimensions, gained popularity, that researchers started exploring the consequences of extra dimensions for black hole topology.
Einstein’s equations, which generate black holes, are notorious for their complexity. They comprise 10 interdependent nonlinear differential equations and can only be explicitly solved under extremely symmetrical circumstances, which makes them very challenging to work with.
In 2002, Roberto Emparan and Harvey Reall, both physicists respectively affiliated with the University of Barcelona and the University of Cambridge, discovered a symmetrical solution to the Einstein equations for a black hole in five dimensions (four of space plus one of time), thirty years after Hawking’s discovery. The object, which they named a “black ring,” is a three-dimensional surface that resembles a donut’s general shape. Although it’s tricky to picture a three-dimensional surface in a five-dimensional space, imagine a circle, and for every point on the circle, substitute a two-dimensional sphere.
The result of combining a circle and spheres creates a solid, irregular doughnut-shaped object in three dimensions. These doughnut-like black holes could theoretically form if they were spinning at an optimal speed, as discovered by Emparan and Reall. “If they spin too fast, they would break apart, and if they don’t spin fast enough, they would go back to being a ball,” noted Jordan Rainone, a Stony Brook math PhD and co-author of a recent paper on black holes. “Emparan and Reall found a sweet spot: Their ring was spinning just fast enough to stay as a doughnut.”
Upon learning about the discovery of the doughnut-shaped black hole, Jordan Rainone, a topologist, found inspiration and expressed hope, stating that “it would be uninteresting if all planets, stars, and black holes in our universe had a spherical shape.”
A New Focus
In 2006, the exploration of non-spherical black holes really took off. That year, Greg Galloway from the University of Miami and Richard Schoen from Stanford University extended Hawking’s theorem to encompass all possible shapes that black holes could have in dimensions greater than four. Lens spaces, a type of mathematical structure that has long been significant in both geometry and topology, were included among the permitted shapes, along with the well-known sphere and the previously demonstrated ring. According to Khuri, “among all the conceivable shapes that the universe could offer us in three dimensions, the sphere is the simplest, and lens spaces are the next most straightforward case.”

According to Khuri, lens spaces can be described as “spheres that have been folded up in a very complicated way.” To comprehend this concept, let’s begin with a simpler shape, like a circle. Split the circle into top and bottom halves. Then, move every point in the bottom half to the diametrically opposite point on the top half. This results in a smaller circle with half the circumference of the original, along with two antipodal points, one at each end of the semicircle, which must be joined.
Moving on to two dimensions, we encounter more complexity. Start with a two-dimensional sphere, or a hollow ball, and move every point on the bottom half until it touches the antipodal point on the top half. This leaves us with only the top hemisphere. However, the points along the equator must also be “identified” or attached to one another. Because of the crisscrossing involved, the resulting surface becomes extremely twisted.
Lens spaces are typically discussed in the context of three dimensions. To better understand them, let’s begin with a basic example involving a solid sphere, which includes both surface and internal points. Imagine two longitudinal lines that run from the north to the south pole and divide the sphere into two halves or hemispheres, one to the East and the other to the West. Then, identify the points on one hemisphere with their antipodal points on the other hemisphere.
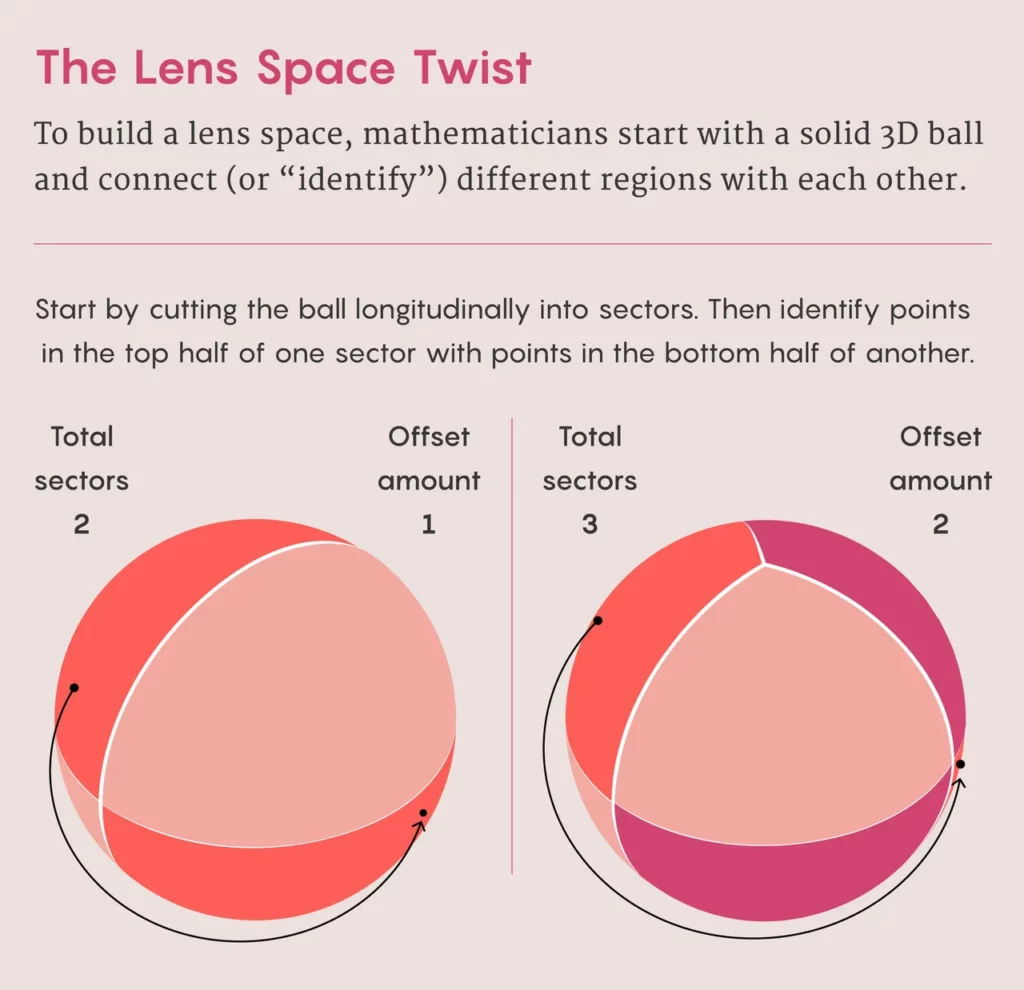
Mathematicians use the notation L(p, q) to refer to a lens space, which is a three-dimensional globe divided into sectors that are connected in specific ways. The number p indicates the number of sectors or hemispheres, and q tells how they should be connected. L(2, 1) is an example of a lens space with two hemispheres connected by antipodal points. As the number of sectors increases, there are more ways to connect them, resulting in increasingly complex shapes. The amount of twisting required is determined by q. Hari Kunduri, a mathematical physicist at McMaster University, explained that these objects are treated mathematically because visualizing them can be challenging. The power of abstraction allows mathematicians to work without drawings.
All the Black Holes
Kunduri and James Lucietti from the University of Edinburgh demonstrated the existence of a black hole in the L(2,1) class in five dimensions in 2014.
Their solution, called a “black lens,” possesses several important qualities. It describes a space-time that is “asymptotically flat,” meaning that the curvature of space-time that would be high near a black hole approaches zero as one moves towards infinity. This characteristic guarantees the physical significance of the results. Kunduri explained that creating a black lens is not challenging, but achieving a flat space-time at infinity is the difficult part.
Emparan and Reall’s black ring is kept from collapsing on itself by its rotation, and the Kunduri-Lucietti black lens must also spin to maintain its structure. However, Kunduri and Lucietti added a “matter” field in the form of an electric charge to help stabilize their lens. Khuri and Rainone’s paper, published in December 2022, takes the Kunduri-Lucietti result as far as possible by proving the existence of black holes with lens topology L(p, q) in five dimensions, for any p and q greater than or equal to 1, provided that p is greater than q and the two numbers share no prime factors.

Khuri and Rainone have pushed the generalization of the Kunduri-Lucietti result to an extreme level in their December 2022 paper. They have demonstrated the possibility of creating a black hole of any lens space shape, in any higher dimension, where the values of p and q satisfy the same conditions mentioned earlier, resulting in an infinite number of black holes in an infinite number of dimensions. However, as Khuri highlighted, the lens space in higher dimensions forms only one part of the overall topology of the black hole, making it even more intricate than the already complicated lens space.
The Khuri-Rainone black holes can have rotation, but it’s not mandatory. Their solution also describes an asymptotically flat space-time. However, to maintain the shape of the black holes and prevent any defects or anomalies that would undermine their findings, they needed a distinct kind of matter field composed of particles associated with higher dimensions. Like the black ring, the black lenses they created have two independent rotational symmetries (in five dimensions) that simplify solving the Einstein equations. Rainone stressed that this assumption simplifies the analysis, but without it, their paper would not exist.
Kunduri, a professor at the University of Florida, praised the work of Khuri and Rainone, saying that their approach allows for all possibilities to be explicitly realized, given the appropriate rotational symmetries. Galloway was similarly impressed by their strategy, which involved embedding the black hole in a higher-dimensional space-time before contracting it to five dimensions while maintaining the desired topology. According to Kunduri, the procedure is very general and can be applied to all possibilities at once.
Khuri is now exploring whether lens black hole solutions can remain stable in a vacuum without matter fields to support them. This is an open question, as a 2021 paper by Lucietti and Tomlinson only offered computational evidence to suggest that a matter field is required. Meanwhile, physicists continue to ponder whether our universe has more than three dimensions of space and one of time. Khuri suggests that the detection of exotic, nonspherical black holes would be evidence that general relativity is valid in higher dimensions, and that our universe has more than four dimensions.
Original story reprinted with permission from Quanta Magazine, an editorially independent publication of the Simons Foundation whose mission is to enhance public understanding of science by covering research developments and trends in mathematics and the physical and life sciences.
Do not forget to share your opinion with us to provide you with the best posts !




0 Comments